Data-Mining – DatenanalyseMethoden für deskriptive Statistik und Datenanalyse

Worum geht es bei deskriptiver Statistik für die Datenanalyse im Unternehmen?

Statistik ist in der Mathematik ein weites Feld, im Unternehmenskontext wird jedoch in der Regel nur ein Bruchteil davon benötigt. Beim Data-Mining geht es zunächst speziell um deskriptive Statistik.

„Deskriptiv“ meint beschreibend. Das Data-Mining soll eine beschreibende Zusammenfassung von Daten liefern. Diese Zusammenfassung kann mit Zahlen oder Grafiken erfolgen, beide Varianten haben ihre jeweiligen Vor- und Nachteile.

Dafür ist ein Grundverständnis von Statistik im Berufsleben hilfreich, wenn nicht sogar notwendig. Sie müssen sich jedoch nicht mit mathematischen Formeln quälen – das übernehmen heutzutage Statistiksoftware, KI oder einfach Excel.

Woher kommen die Daten für die deskriptive Statistik?

Um deskriptive Statistik anwenden zu können, werden zuerst Daten benötigt, die beschrieben werden sollen. In Unternehmen und im Hinblick auf betriebswirtschaftliche Fragen entstehen Daten in unterschiedlichsten Varianten aus unterschiedlichsten Quellen.

Beispiele sind Daten aus:

• Produktionsprozessen: Rüstzeiten, Durchlaufzeiten, produzierte Stückzahlen
• Qualitätskontrolle: Produktfehler, Abweichungen bei Prozessparametern, Nacharbeit, Ausschuss
• Materialwirtschaft: Energieverbrauch, Materialverbrauch, Abfall
• Buchhaltung: Rechnungen, Rechnungsbeträge, Zahlungen
• Vertrieb: Angebote, Bestellungen, Erstkäufe, Warenkörbe
• Marketing: Response-Raten, Kundenmerkmale, Marktdaten, Wettbewerbsdaten
• Kundenservice: Beschwerden, Anrufe im Callcenter

Im Folgenden sollen die Möglichkeiten des Data-Minings und der Datenanalyse am Beispiel eines Callcenters erläutert und illustriert werden.

Beispiel für Datenanalyse: Datenquelle Callcenter

Die Telefonanlage des Callcenters erfasst für jeden Anruf

• Wochentag des Anrufs
• Zeitpunkt (Stunde)
• Verweildauer in der Warteschleife (Wartezeit)
• Dauer des Gesprächs
• das Anliegen
• den Mitarbeiter, der sich um das Anliegen kümmert

Einmal in der Woche werden diese Daten als Wochenstatistik analysiert, um ein definiertes Qualitätsniveau den Kunden gegenüber sicherstellen zu können. Dazu wird insbesondere auf die Verweildauer in der Warteschleife geachtet.

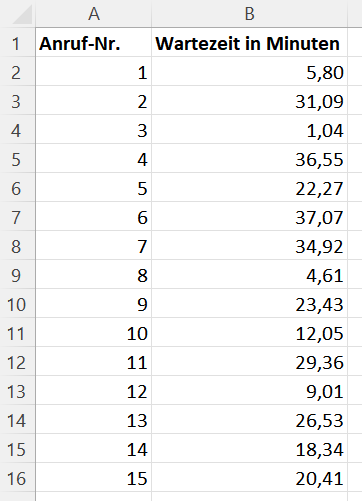
Der Beispieldatensatz der laufenden Woche im Callcenter enthält insgesamt 19.155 Anrufe. Einen kleinen Ausschnitt aus dem Datensatz zeigt die folgende Tabelle.

Statistische Kennzahlen zur Datenbeschreibung

Für einen ersten groben Überblick verwendet die deskriptive Statistik eine Fünf-Punkte-Zusammenfassung, welche die wichtigsten Lageparameter darstellt. Mithilfe von Lageparametern wird die Verteilung der Datenpunkte beschrieben; „wie die Daten liegen“.

Die fünf Lageparameter der Fünf-Punkte-Zusammenfassung für einen Datensatz sind:

• Minimalwert
• Maximalwert
• Mitte
• erstes Quartil
• drittes Quartil

Diese Lageparameter werden folgendermaßen ermittelt und mit Excel-Funktionen berechnet:

Minimalwert und Maximalwert

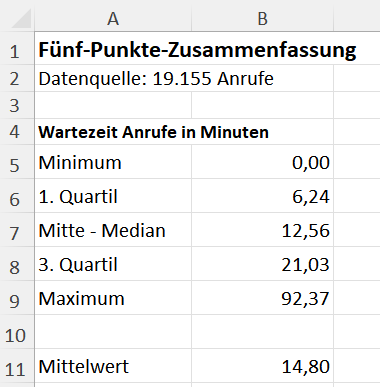
Für die Wartezeit des Kunden am Telefon zeigt die Analyse den Minimalwert 0 Minuten und den Maximalwert 92,37 Minuten. In Excel gibt es dafür die Funktionen MIN() und MAX(), die nur die Wartezeit des Datensatzes (Spalte B in der Tabelle) als Parameter benötigen.

Mitte der Verteilung

Der nächste Lageparameter beschreibt die Mitte der Verteilung. Dabei ist Vorsicht geboten, da es zwei unterschiedliche Arten der Mitte gibt:

• arithmetisches Mittel, auch als Durchschnitt oder Mittelwert bezeichnet
• Median

Der umgangssprachliche Durchschnitt als arithmetisches Mittel ist anfällig für Ausreißer, also für einzelne extreme Werte an den Enden der Verteilung.

Besonders deutlich wird das zum Beispiel bei Einkommensverteilungen. Wenn in einem kleinen Ort ein Milliardär wohnt, ist das Durchschnittseinkommen sehr hoch – obwohl nur eine Person extrem viel Einkommen erzielt und alle anderen vielleicht sogar sehr wenig.

Eine höhere Aussagekraft hat hier der Median, der den mittleren Wert einer Verteilung beschreibt. Mittlerer Wert bedeutet, dass die Hälfte der Werte darüber liegt und die andere Hälfte darunter. Der eine Milliardär würde also den Median nicht verschieben, da die Mitte der Einkommen sich nicht verändert.

Diese Unterscheidung gibt es in Excel auch. Die Funktion MITTELWERT() berechnet das arithmetische Mittel, die Funktion MEDIAN() entsprechend den Median.

Die Wartezeiten des Callcenters haben einen Mittelwert von 14,80 Minuten und einen Median von 12,56 Minuten. Aus der Differenz der Werte lässt sich schon erahnen, dass es wohl ein paar Ausreißer nach oben gibt, denn das arithmetische Mittel ist größer als der Median.

Quartile

Die zwei weiteren Kennzahlen zur Fünf-Punkte-Zusammenfassung sind das erste und das dritte Quartil. Der Name Quartil impliziert bereits eine Vierteilung des Datensatzes – und genau das ist es auch.

Das erste Quartil enthält 25 Prozent der Datenpunkte des Datensatzes, das dritte Quartil dementsprechend 75 Prozent. Prinzipiell könnte der Median auch als 50-Prozent-Quartil aufgefasst werden, diese Bezeichnung ist aber unüblich.

Für die Berechnung der Quartile bietet Excel eine passende Funktion: QUARTILE.INKL().

Bei der Auswahl der Formel ist Vorsicht geboten, Excel kennt sowohl QUARTILE.INKL() als auch QUARTILE.EXKL(). Beide Formeln unterscheiden sich etwas in Details der Berechnung, was im Normalfall aber keinen Unterschied im Ergebnis ausmacht.

Da jedoch die zwei bei Datenanalysen beliebten Programmiersprachen R und Python die Quartile nach der gleichen Formel wie QUARTILE.INKL() berechnen, sollten Sie diese verwenden.

Für den Beispieldatensatz aus dem Callcenter sind die Werte: 6,24 Minuten für das erste Quartil und 21,03 Minuten für das dritte. Das bedeutet, dass 25 Prozent der Anrufer weniger als 6,24 Minuten und 75 Prozent der Anrufer nicht länger als 21,03 Minuten warten.

Tabellarische Datenanalyse

Diese beschreibenden Kennzahlen des Datensatzes aus dem Callcenter sind in der folgenden Tabelle aufgeführt. Da nur die Werte für die fünf beschreibenden Kennzahlen genannt sind, wird dies auch als tabellarische Analyse der Daten bezeichnet.

Grafische Datenanalyse

Diese fünf Werte (ohne Durchschnitt) lassen sich auch in einer Grafik darstellen, dem sogenannten Boxplot.

In der Statistik werden Boxplots häufig verwendet, um die Verteilung von Daten grafisch sichtbar und besser verständlich zu machen. Bequemer Weise bringt Excel seit der Version 2016 auch eine Diagrammvorlage dafür mit.

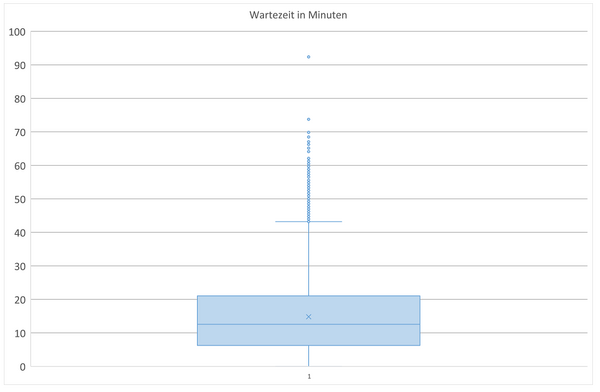
Um einen Boxplot zu erstellen, müssen Sie nur die Datenreihe mit den Wartezeiten markieren und im Menüband Einfügen > Diagramme > Empfohlene Diagramme > Registerkarte Alle Diagramme > Kastengrafik wählen. Das Ergebnis für den Datensatz mit den 19.155 Werten zeigt die folgende Abbildung.

Mit dem Boxplot-Diagramm Lageparameter visualisieren

Der Ausreißer nach oben sticht sofort ins Auge. Ein Anrufer hat mehr als 90 Minuten gewartet – das ist das Maximum von 92,37 Minuten. Es ist aber beruhigend zu sehen, dass das tatsächlich ein extremer Ausreißer ist, die anderen einzelnen Punkte sind zwar auch Ausreißer, aber nicht so extreme.

In der Mitte des Diagramms ist eine blaue Box, die dem Diagramm den Namen gibt. In dieser Box sind dargestellt:

• der Median als horizontale Linie; hier liegt die Mitte der Verteilung, 50 Prozent der Messwerte unterhalb dieser Linie, 50 Prozent darüber
• der Durchschnitt oder Mittelwert ist mit einem kleinen Kreuz markiert, was zwar nicht der statistischen Definition eines Boxplots entspricht, aber auch nicht stört

Die blaue Box repräsentiert die mittleren 50 Prozent der Verteilung. Ihre untere Begrenzung wird vom ersten Quartil gebildet, die obere vom dritten.

Oben und unten ragen aus der Box noch Linien, die sogenannten „Antennen“, „Fühler“ oder „Whiskers“ heraus. Die Länge der Fühler ist 1,5-mal die Höhe der Box; der sogenannte Interquartilsabstand oder IQR. Alle Werte, die noch weiter weg sind, werden als Ausreißer bezeichnet; sie sind als einzelne Punkte im Diagramm dargestellt.

Ein Boxplot enthält also die gleichen Informationen wie eine Fünf-Punkt-Zusammenfassung, ist jedoch grafisch schneller zu erfassen. Man sieht auf den ersten Blick:

• die Streuung der Datenpunkte,
• wie weit die Messwerte reichen,
• ob es Ausreißer gibt und
• in welchem Wertebereich die meisten Daten liegen.

Histogramm zur Datenanalyse

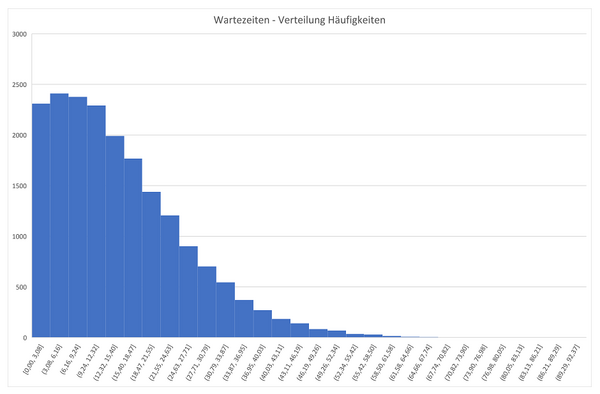
Man kann in einem Boxplot allerdings nur die Streuung der Datenpunkte sehen, nicht die Verteilung – wie viele Kunden also wie lange gewartet haben. Das erkennt man gut in einem Histogramm,

• in dem die Werteskala (die Minuten) in einzelne gleich große Bereiche eingeteilt wird (x-Achse) und
• die Höhe eines Balkens angibt, wie viele Datenpunkte in dem jeweiligen Bereich liegen (y-Achse).

Zum Glück gibt es dafür eine Vorlage in Excel. Im Menüband Einfügen > Diagramme > Empfohlene Diagramme > Registerkarte Alle Diagramme > Histogramm.

Mit dieser Diagramm-Vorlage teilt Excel die Werte in Klassen oder Wertebereiche ein (x-Achse) und zählt, wie viele Werte in diesen Bereich fallen; diese Anzahl wird als Säule angezeigt (y-Achse). Sie können die Klassengröße auf der x-Achse in Excel einstellen.

Mit dem Histogramm in der folgenden Abbildung können Sie erkennen, dass ein großer Teil der Anrufer nicht länger als 21 Minuten wartet. Das ist keine Überraschung, das 3. Quartil liegt schließlich bei 21,03 Minuten. Und die Anzahl der Anrufer mit langer Wartezeit nimmt danach rapide ab.

Mit den beiden Diagrammen, Boxplot und Histogramm, können Sie eine ganze Menge aus Ihren Daten ablesen. Und je nachdem, für welchen Einsatzzweck Sie analysieren, sind die Lageparameter als Zahlen oder als übersichtliche Grafik vorteilhafter.

Auch wenn das nur grundlegende Werkzeuge der Statistik sind, können Sie mit diesen Mitteln schon erstaunlich viele Informationen für unternehmerische Entscheidungen aus Ihren Daten gewinnen.